Sigmod 论文《Revisiting the Design of In-Memory Dynamic Graph Storages》阅读
本论文来自上海交大,论文主要关于内存中动态图存储(In-Memory Dynamic Graph Storage, DGS)设计的研究论文,论文核心是通过系统评估现有 DGS 方法,揭示其性能瓶颈并指明未来优化方向。动态图存储需支持并发读写,以满足实时图分析和更新需求。现有方法(如 LLAMA、Aspen、LiveGraph、Teseo、Sortledton 等)在读写支持、空间开销和并发控制上差异显著,但缺乏对这些维度权衡的系统研究。作者主要分析了现有系统的设计,以及讨论了如何针对 DGS 算法进行系统评估。
本文阅读该论文的重点一是仔细学习作者类比、分析、抽象系统的做法,二是借作者之手,对现在的 DGS 系统的发展做一个简单的了解。
论文链接 Revisiting the Design of In-Memory Dynamic Graph Storages
现有 DGS 方法的核心差异体现在图容器(存储结构)和并发控制(版本管理与协议)两方面:
| Method | Version Management | Protocol | Vertex Index Container | Neighbor Index Container | Additional Optimization |
|---|---|---|---|---|---|
| LiveGraph | Fine-Grained with Continuous Version | S2PL | Dynamic Array | Dynamic Array | Bloom Filter |
| Sortledton | Fine-Grained with Version Chain | G2PL | Dynamic Array | Segmented Skip List | Adaptive Indexing |
| Teseo | Fine-Grained with Version Chain | OCC | Hash Table | PMA | Write-Optimized Segment |
| Aspen | Coarse-Grained | Single Writer | AVL Tree | Segmented PAM | Vertex Index Flatten & Data Encoding |
| LLAMA | Coarse-Grained | Single Writer | Dynamic Array | Dynamic Array | - |
省流结论
作者通过测试图容器效率、并发控制粒度及内存消耗,得出以下结论:
- 空间开销大:现有 DGS 方法内存消耗显著高于静态存储(如 CSR)。例如,Aspen 比 CSR 高 3.3-10.8 倍,最优细粒度锁方法高 4.1-8.9 倍;
- 硬件利用不足:现有方法忽略现代架构的内存访问特性,分段存储导致缓存 Cache misses 增加、分支预测错误率上升,性能低于连续存储;
- 细粒度锁并发控制的问题:能提升写吞吐量,但因维护每个邻接的版本和锁检查,导致效率和空间开销大,且高 degree 顶点存在严重锁竞争;
- CSR 仍占优:静态存储 CSR 在查询性能(高 2.4-11.0 倍)和内存消耗上显著优于现有 DGS 方法;
所以作者认为接下来的发展方向应该是:
- 优化版本管理:减少细粒度锁版本的空间和效率开销,探索更粗粒度锁的版本控制;
- 提升硬件利用率:优化内存布局以减少缓存 misses 和分支错误,结合向量化等硬件特性;
- 改进并发控制:降低读写干扰,缓解高 degree 顶点的锁竞争,提升插入可扩展性;
图表示
静态图与动态图:静态图可表示为邻接表(AdjLst)或压缩稀疏行(CSR)格式,其中 CSR 因紧凑的内存布局和高效的访问性能,成为静态图最常用的存储方式。动态图则通过初始图$G_0$和一系列更新$\Delta G$(包括顶点 / 边的插入或删除)来记录图的演化,每次更新后形成新的图版本$G_i$。
顶点与边的表示:顶点 ID 被限定在$[0, |V|)$的整数范围内,以提高计算和存储效率,若输入 ID 不符合该范围,可通过字典编码映射。
CSR 格式
CSR需要三个数组表示矩阵结构
- V = [] # 存储非零元素的值:
- COL_INDEX = [] # 存储每个非零元素所在的列号
- ROW_INDEX = [] # 存储每行首个非零元素在V中的位置
要获取第row行的非零元素:
- 计算起始位置:
a = ROW_INDEX[row] - 计算结束位置:
b = ROW_INDEX[row+1] - 该行元素在V中的区间为:
V[a : b] - 对应的列号在:
COL_INDEX[a : b]
📌 重要特性:
元素V[k]的行号=row,列号=COL_INDEX[k]
其中k ∈ [ROW_INDEX[row], ROW_INDEX[row+1])
顶点集的数据结构
| Data Structure | INSERT | SEARCH | SCAN | RESIZE | Space |
|---|---|---|---|---|---|
| Dynamic Array | $O(1)$ | $O(n)$ | $O(n)$ | $Θ(n)$ | $O(n)$ |
| Sorted Dynamic Array | $O(n)$ | $O(log n)$ | $O(n)$ | $Θ(n)$ | $O(n)$ |
| Packed Memory Array | $O(log² n)$ | $O(log n)$ | $O(n)$ | $Θ(n)$ | $O(n)$ |
| Skip List | $O(log n)$ | $O(log n)$ | $O(n)$ | - |
$O(n log n)$ |
| Hash Table | $O(1)$ | $O(1)$ | $O(n)$ | - |
$O(n)$ |
| AVL Tree | $O(log n)$ | $O(log n)$ | $O(n)$ | - |
$O(n)$ |
| Parallel Augmented Map | $O(log n)$ | $O(log n)$ | $O(n)$ | - |
$O(n)$ |
这里再来复习一下上述数据结构中的常见CURD时间复杂度,其中:
- 动态数组:支持快速追加插入$O(1)$和连续扫描,但搜索需遍历(O(n)),扩容时需复制元素(\Theta(n));
- 排序动态数组:通过二分查找优化搜索(O(\log n)),但插入需移动元素(O(n));
- 其他结构:PMA平衡了插入和搜索效率;跳表和 AVL 树在插入、搜索上均为(O(\log n)),但跳表空间开销较高(O(n \log n));哈希表支持常数级插入和搜索,但扫描效率低(O(n))。
动态图抽象模型
抽象模型
作者从 “图查询与数据抽象” 和 “图操作抽象” 两个维度,揭示了动态图存储的核心逻辑,先来看“图查询和数据抽象”:
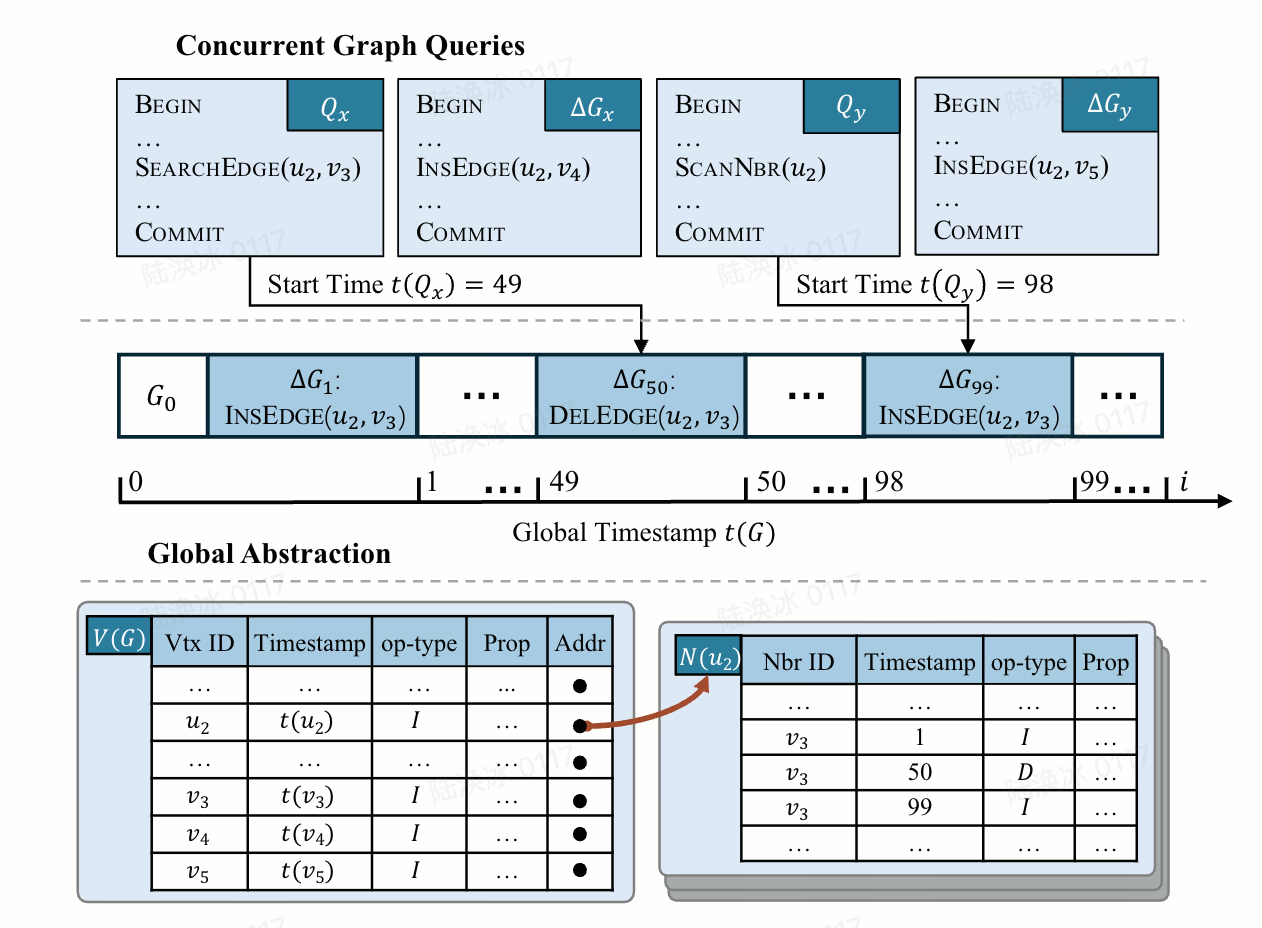
这张图展示了 DGS 的多层抽象模型,包括 Global Abstraction和 Local Abstraction,用于统一建模图的查询时序、数据结构及版本管理逻辑:
Global Abstraction核心逻辑:通过 “全局时间戳”((t(G)))协调读(Q)与写((\Delta G))的关系,确保并发操作的可串行化。全局时间戳(t(G))初始为 0,仅在写提交时递增(如(\Delta G_1)在(t(G)=1)提交,(\Delta G_2)在(t(G)=2)提交)。读Q的 “本地时间戳”((t(Q)))等于其开始时的全局时间戳(如(Q_1)在(t(G)=49)开始,(t(Q_1)=49)),仅能访问时间戳≤(t(Q))的版本数据。
Local Abstraction核心逻辑:将图数据拆解为 “顶点表”((V(G)))和 “邻接表”((N(u))),每个条目记录版本信息,体现数据的动态演化。具体的:
- 顶点表:每个顶点条目包含 “顶点 ID”、“时间戳”、“操作类型”(I = 插入 / D = 删除)“属性”“邻接表地址”;
- 邻接表:每个邻接条目包含 “邻接 ID”、“时间戳”、“操作类型”、“属性”,记录边的版本变化(如(v_3)在(t=1)插入、(t=50)删除、(t=99)再次插入)。
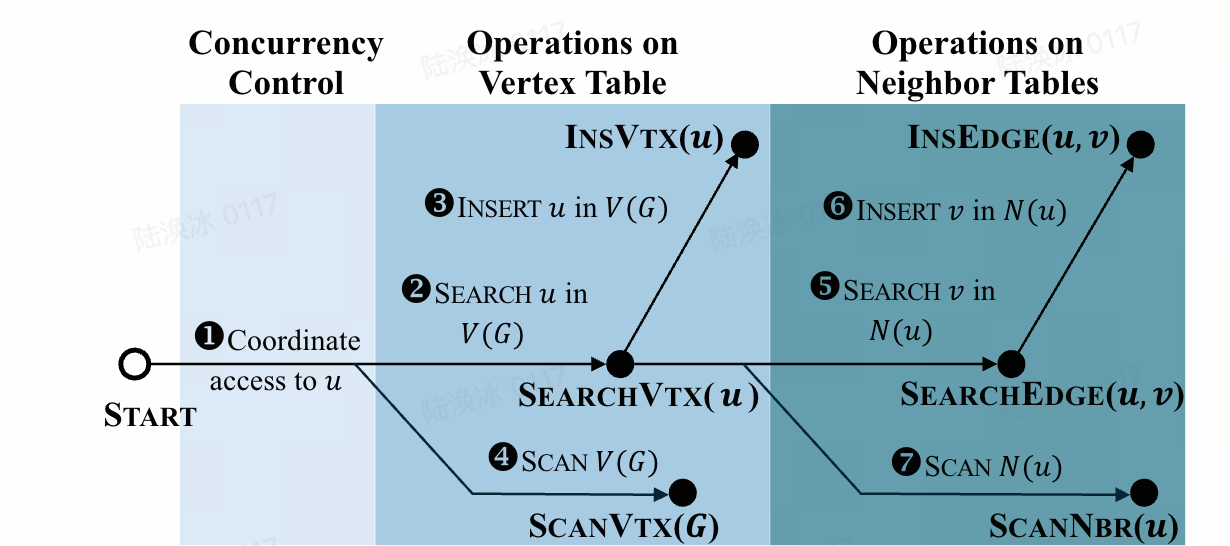
这张图展示了各类图操作(如插入顶点、插入边、查询边、扫描邻接等)的执行流程,揭示了操作之间的依赖关系及底层数据访问路径。核心逻辑所有操作始于 “START” 节点,通过 “顶点表操作”((P_V))和 “邻接表操作”((P_N))的组合完成,路径中包含 “查找”、“插入”、
“扫描” 等基本操作。
比如:插入边(((u, v)))需先 “搜索顶点u是否存在”(((u))),再 “搜索v是否在(N(u))中”(((u, v))),最后 “插入v到(N(u))”。扫描邻接(((u)))需先 “搜索顶点u”(((u))),再 “扫描(N(u))的所有条目”。
LiveGraph具体应用
正如作者上述抽象的所述,LiveGraph 每个写(如插入 / 删除边)提交时会更新全局时间戳,并为操作的顶点 / 邻边创建新的版本(标记 begin-ts 为当前全局时间戳);读(如扫描邻边)仅访问 begin-ts≤自身本地时间戳且 end-ts=INF(未删除)的版本,符合Global Abstraction的时序协调逻辑。
而LiveGraph 为每个顶点和邻边维护 “begin-ts”和 “end-ts”,与Local Abstraction中的 “时间戳” 和 “操作类型” 对应。例如,邻接表中(v_3)的多个版本((t=1)插入、(t=50)删除、(t=99)插入),正是 LiveGraph 通过连续版本存储实现动态更新的具体表现。
LiveGraph 的操作流程也符合操作的抽象路径:
- 插入边:依赖动态数组的 “搜索”(遍历邻边表检查v是否存在,辅以布隆过滤器优化)和 “追加插入”(在 DA 末尾添加新版本),对应上图 中 InsEdge 的路径。
- 扫描邻边:直接遍历动态数组的连续存储,从末尾向开头访问(优先最新版本);
- 并发控制:LiveGraph 对每个顶点加锁(S2PL),确保操作的线程安全。
作者从 “时间戳协调” 和 “版本化数据结构” 角度,结合LiveGraph解释了一般动态图如何通过细粒度锁局部时间/版本(begin-ts/end-ts)和全局时间戳实现并发读写;并结合 LiveGraph 的动态数组,解释了如何依赖S2PL支持插入、扫描等操作。
目前主流动态图的做法
现有DGS方法主要致力于优化两个问题:
- 图并发控制,包括版本管理和协调并发图查询执行的并发控制协议,以及最小化每个图操作的开销;
- 图容器,包括顶点索引、邻边索引和其他内存数据结构优化措施;
Live Graph
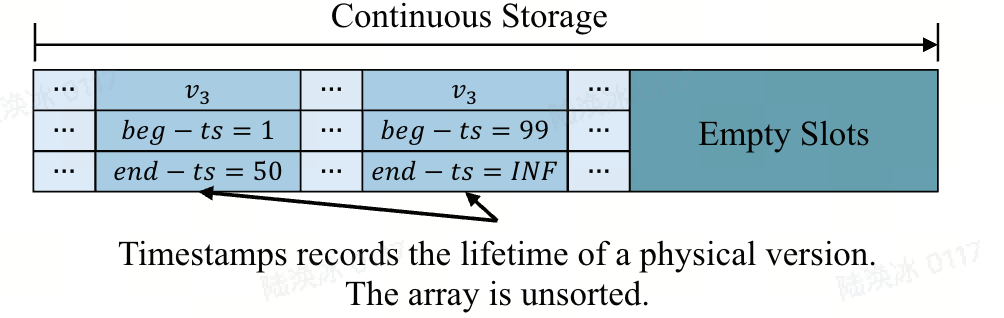
图并发控制:LiveGraph 为顶点集(V(G))中的每个顶点配备一个锁,并采用S2PL来同步数据访问。对于写(\Delta G),LiveGraph 首先获取(\Delta V)((\Delta G)中涉及的顶点)中所有顶点的排他锁,执行图操作后再释放这些锁。为处理死锁,若在时限内无法获取锁,LiveGraph 会中止(\Delta G)。如上图所示,LiveGraph 为每个邻边或顶点的版本记录开始和结束时间戳((begin-ts)和(end-ts)),以记录其生命周期。对于在时间戳i提交的(\Delta G),插入边(InsEdge((u, v)))会查找(N(u))中v的最新版本。若找到,将其(end-ts)设为i,并创建一个(begin-ts = i)且(end-ts = INF)的v的新版本;若未找到,则直接创建v的新版本。删除边操作(DelEdge((u, v)))会查找v的最新版本并将其(end-ts)设为i。对于读Q中的操作,LiveGraph 会获取顶点的共享锁,并在操作完成后立即释放。例如,遍历邻边操作(((u)))获取u的锁,基于时间戳访问邻边后立即释放锁。因此,Q不会导致死锁,因为它从不同时持有两个锁。
图容器:对于(u \in V(G)),LiveGraph 使用动态数组作为(N(u))的邻边索引,其中每个元素对应(v \in N(u))的一个物理版本。由于动态数组的存储是连续的且不存在版本链,遍历操作(Scan)速度很快。此外,LiveGraph 从动态数组的末尾向开头执行遍历,因为最新元素可能比旧元素更频繁地被访问。因为动态数组是未排序的,需要通过遍历执行搜索,所以插入边也较慢,因为它依赖于查找边操作。为缓解这一问题,LiveGraph 为每个(N(u))维护一个布隆过滤器,用于记录元素是否存在于(N(u))中。LiveGraph 的顶点索引(V(G))也使用动态数组。由于顶点 ID 的范围是([0, |V|)),索引u处的元素即为顶点u,因此顶点索引的查找操作时间复杂度为(O(1))。
Sortledton
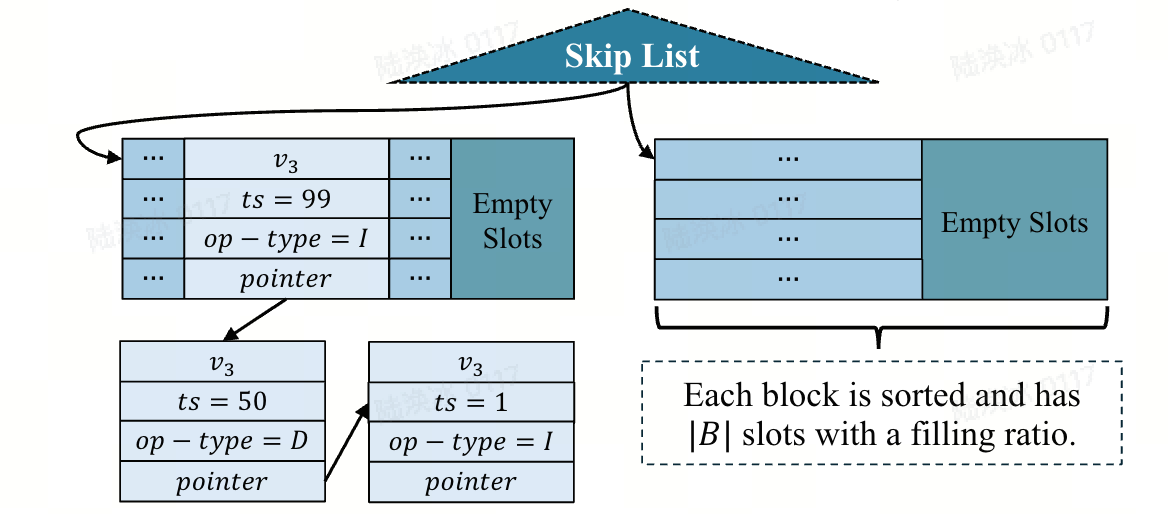
图并发控制:Sortledton 同样使用S2PL,但对加锁顺序进行了优化: 将(\Delta V)中的顶点按顶点 ID 升序排序,并按该顺序获取它们的排他锁。这种优化通过避免写之间的循环等待来防止死锁,因此 Sortledton 不需要任何处理死锁的机制。对于在时间戳i提交的(\Delta G)中的插入边(InsEdge((u, v)))(或删除边操作(DelEdge((u, v)))),Sortledton 会创建一个时间戳为i、操作类型为 I(或 D)的v的新版本,如上图所示。Sortledton 为v的不同版本维护一个版本链,新版本指向旧版本。对于读,Sortledton 采用与 LiveGraph 相同的并发控制策略。
图容器:与 LiveGraph 类似,Sortledton 使用动态数组作为顶点索引。对于邻边索引,Sortledton 将(N(u))划分为块B,并使用跳表作为链接这些块的块索引。每个块的填充率维持在 50% 到 100% 之间。当一个块满时,Sortledton 将其分裂为两个块,平均分配邻边;若填充率低于 50%,则将其与相邻块合并。每个块的第一个元素作为其在跳表中的键,这种结构称为分段跳表。读操作通过遍历版本链查找目标版本。而真实世界的图通常是稀疏的,Sortledton 也给了一种优化手段:自适应邻边索引:若(N(u))的大小低于阈值(如 256),则使用排序动态数组作为邻边索引,而非分段跳表。
Teseo
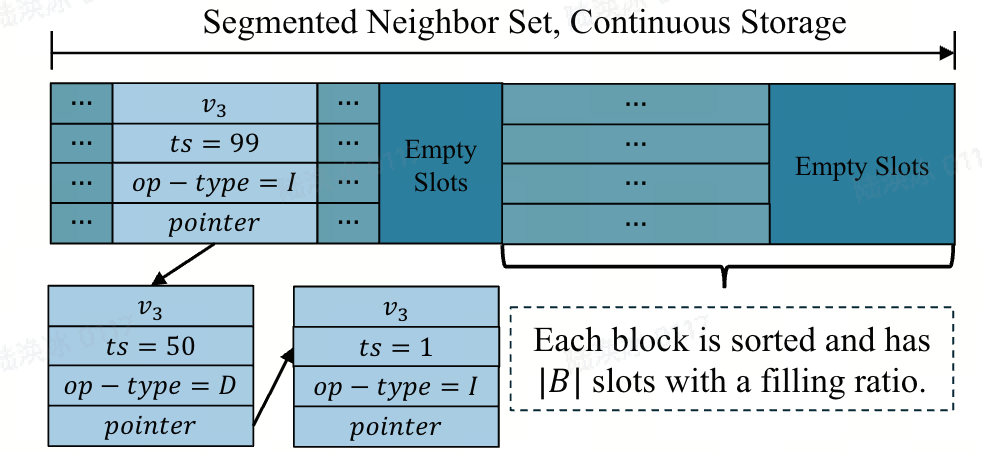
图并发控制:Teseo 采用与 Sortledton 相同的版本管理方法,但采用OCC来协调并发写。与 LiveGraph 和 Sortledton 为每个顶点配备一个锁不同,Teseo 为每个边分区维护一个锁,以同步并发数据访问。具体的,Teseo 将(E(G))逻辑划分为大小相等的分区,每个分区配备一个锁。写在访问分区中的数据前,会获取该分区的排他锁(读则获取共享锁),并在访问后立即释放。
图容器:如上图所示,Teseo 使用PMA作为邻边索引,但将所有邻接表存储在单个 PMA 中。若(N(u))较大,它会跨越 PMA 中的多个块;而多个小邻边集可以共享一个块。然而,若将(E(G))存储在一起,PMA 的全局重平衡开销会很大。为解决这一问题,Teseo 将单个 PMA 划分为多个大叶子节点(每个几兆字节),并使用ART为这些叶子节点建立索引,将这种数据结构称为 FAT。除此之外,Teseo 使用哈希表作为顶点索引,记录每个顶点的邻边索引在 FAT 中的位置。默认情况下,FAT 中的块是排序的,为读优化段;当插入率较高时,FAT 会切换到写优化段,通过追加到更新日志来处理更新。对于写优化段,Teseo 通过遍历段来查找目标顶点。
Teseo的做法有点类似lucene中的ART状态机的做法,并且切换读优化段和写优化段的做法在很多数据库中都见到过。
PMA
PMA 的核心思想是在物理连续的内存块中,有意地预留一些“间隙”。这些间隙分布在数组元素之间。PMA 中的元素并不是像传统数组那样一个紧挨着一个。它们之间散布着一些空的槽位(Gaps)。这些间隙并不是随机分布的。它们通常按照某种策略(例如,基于元素数量或位置)分布在数据块中。一种常见的策略是让间隙的密度随着位置的变化而变化(例如,在数据块的开头和结尾间隙较少,中间较多),或者均匀分布。
- 插入操作:当需要插入一个新元素时,算法会找到一个目标附近的间隙来放置它。如果附近没有合适的间隙,或者间隙密度低于某个阈值,PMA 不会立即移动所有元素。相反,它会进行一种称为 “重新平衡” 的操作。
- 重新平衡: 这个操作会扫描数据块中的一个局部区域(比整个数组小得多),将该区域内的所有元素(包括新插入的)和现有的间隙重新整理,使它们在该区域内均匀分布(或者满足预设的间隙密度规则)。这个操作的成本分摊到多次插入中,使得单次插入的均摊时间复杂度可以达到 $O(log n)$。
- 删除操作:删除一个元素时,简单地将其标记为“间隙”(或者用一个特殊值标记)。如果某个区域的间隙密度变得过高(超过阈值),也会触发对该区域的重新平衡操作,将间隙移除或重新分布,使数据更紧凑。
- 查找操作:由于数据在物理内存上仍然是连续或近似连续的(间隙是分布其中的),PMA 支持高效的二分查找。查找算法需要跳过遇到的间隙(例如,通过记录元素的实际位置索引或使用特殊的“间隙”标记值)。
Aspen
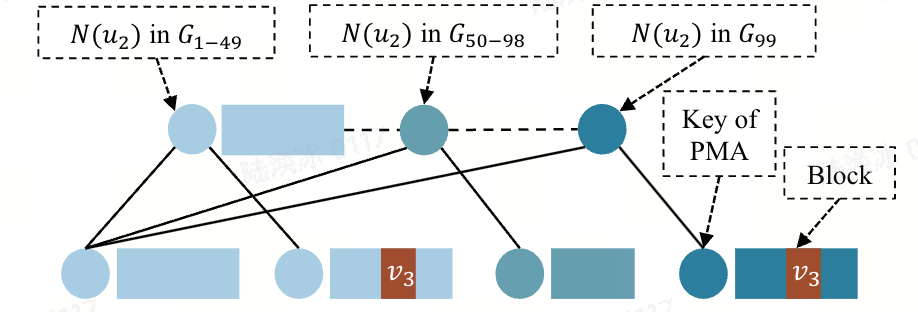
图并发控制:Aspen 采用粗粒度锁策略,为每个图快照维护时间戳。具体的,Aspen 使用单写多读,写串行执行,允许多个读并发执行。写(\Delta G_i)使用CoW方法在图的副本上应用更新,创建新的快照(G_i)。如上图所示,读Q在最新的图快照上执行,所以读和写从不相互阻塞,多个读可以共享同一个图快照。
图容器:Aspen 将(N(u))划分为一组排序的块,为这些块建立索引。插入边u时会复制块,然后复制从该块到根的路径,目的是创建(N(v))的新快照。给定(N(u))和块大小B,Aspen 选择满足(v \mod B = 0)的顶点作为头部,即(heads = {v \in N(u) | v \mod B = 0})。这种方法确保对一个块的更新不会影响相邻块。Aspen 使用 AVL 树作为顶点索引,并为每个更新操作复制树中的路径。
Aspen 提出了两种优化方法来提升性能:第一,对于长时间运行的读,Aspen 可以创建一个基于 AVL 树的数组,存储每个邻接表的位置,以消除 AVL 树中的查找开销;第二,Aspen 使用差分编码方案压缩块中的数据,并使用字节码进行压缩,以加速集合交集运算。
LLAMA
LLAMA 于 2015 年提出,采用与 Aspen 类似机制。具体而言,LLAMA 将顶点表划分为多个分区,每个分区存储在一个数据页中,并维护一个Hash表来存储这些页的位置。每个写必须复制Hash表以创建新的图快照,这种复制开销限制了更新性能和图的可扩展性。
对比分析
时间方面:鉴于顶点 ID 的范围是([0, |V|)),使用动态数组作为顶点索引时,查找顶点和插入顶点操作的时间复杂度为(O(1)),且内存访问简单。由于存储是连续的,动态数组支持快速的遍历操作。相比之下,尽管哈希表和 AVL 树在某些操作上具有相同的时间复杂度,但它们的开销比动态数组更大。由于动态图存储中插入边依赖于查找边操作,因此尽管动态数组的插入操作(Insert)时间复杂度为(O(1)),因为查找边带来的均摊时间复杂度也难以避免。
空间方面:实际内存消耗受元素大小的影响显著。Sortledton 和 Teseo 中的每个元素消耗(3 \times w)字节(w为字长),分别用于存储顶点 ID、版本和指针。操作类型可以使用时间戳的高位表示。LiveGraph 中的每个元素也占用(3 \times w)字节。相比之下,由于采用粗粒度锁,Aspen 中的每个元素仅消耗w字节。此外,Aspen 的邻边索引没有空槽。所以粗粒度锁方法比细粒度锁方法的内存效率更高。
细粒度锁与粗粒度锁的比较:细粒度锁方法需要对每个图操作执行锁操作,这可能导致锁竞争,从而产生高昂的时间成本。高 degree 顶点尤其容易被频繁访问。细粒度锁方法需要对每个元素进行版本检查,这会增加内存数据加载量和版本比较的计算量。相比之下,粗粒度锁方法避免了这些问题。但是细粒度锁方法允许多个写者同时更新图,并通过简单插入新元素原地更新,反而提升整体更新性能。
并且的,细粒度锁锁策略对底层图容器没有特殊要求,因此更具通用性;而粗粒度锁策略需要支持快速创建快照。但由于粗粒度锁策略不为每个元素维护版本或执行版本检查,它可以有效地与数据压缩技术结合,而这对细粒度锁方法来说是不可行的。
总结
该论文围绕内存中 DGS 展开系统研究,旨在通过统一的抽象模型和测试框架,评估现有方法的性能瓶颈并指明优化方向。
研究提出了DGS的多层抽象模型(全局、局部及操作抽象),统一建模图查询、数据及访问模式,并基于此构建了包含第三方模块和自定义沙箱的通用测试框架,实现对 LLAMA、Aspen、LiveGraph、Teseo、Sortledton 等现有方法的公平对比。
实验结果表明,现有 DGS 方法存在显著缺陷:空间开销大;硬件利用不足,分段存储导致缓存失效和分支预测错误率上升;细粒度锁并发控制因版本维护和锁竞争效率低下。
最后,论文指出未来需优化版本管理以减少空间和效率开销、提升硬件利用率,并改进并发控制机制以缓解读写干扰和锁竞争问题。
Sigmod 论文《Revisiting the Design of In-Memory Dynamic Graph Storages》阅读

