数据库事务模型分析(1)—— 计算模型
事务服务的计算模型可以通过多种方法精确创建,和抽象程度有关,而建模数据库事务服务的系统需要遵循一些基本的方法论以及相关实际因素,本系列所作的建模一般分为以下5个步骤:
- 首先定义数据对象的基础操作,这些操作被认为是原子的,并且独立于其他操作,这一步并没有明确定义什么是数据对象以及需要考虑什么类型数据的基础操作。因此本系列定义两种不同的计算模型:页模型和对象模型;
- 对事务以及事务执行顺序建模,将其视为在数据对象上基础操作的一个(全/偏)序列;
- 本系列使用调度或者历史的概念作为对事务执行并发的抽象;
- 在所有句法正确的调度中,必须从中识别出保证ACID“正确”的调度;
- 需要“算法”或者“协议”来即时地创建事务正确的调度,当事务提交之后,可以被动态执行;
上述的“页模型”是一个非常简单的模型,可以观察在存储层中,数据页是如何被事务优雅的读写的。接下来可以看到这个模型以一种非常优雅的方式建模了并发控制和事务恢复的实现,并且可以描述非常多(但不是全部)系统实现中的重要语义。
“对象模型”是预留给数据库的上层操作,比如访问层或者查询处理层的操作,很容易想到把上层数据应用的业务数据对象考虑在内,可以推导出更复杂的对抽象数据结构ADT的语义,借由ADT来执行下层数据对象的操作。
页模型
定义页模型基于一个基本假设:
所有对数据的高层操作都会转化为对数据页的读写操作,并且假设每个页的操作都是不可分的,无论是内存还是在硬盘上。
在用页模型给出事务的一般定义之前,先看一个简化的版本,把事务看作具有全序关系的一组操作步骤,而一般页模型允许偏序关系:
一个事务$t$(在页模型中)是形如$r(x)$或者$w(x)$的操作步骤的有限序列,记作:
$$
t = p_1…p_n
$$
其中,$n < \infty$, 对于$1 \leq i \leq n$,$x \in D$,有$p_i \in {r(x), w(x)}$,这样就从事务执行的细节中抽象出事务执行的读写序列了。
在同一个事务中,操作步骤由$p_i$表示,即事务中第$i$步操作,存在多个事务的情况下,可以给每个事务添加一个唯一的事务id,作为步骤的另外一个下标,$p_{ij}$就代表了第$i$个事务的第$j$步,但是在页模型中为了简化问题,可以简单的从上下文推断出第几步,因此不显式给出步数。
只考虑一个事务,可以表示为:
$$
p_j = r/w(x)
$$
理解为事务第$j$步读/写页数据。实际上,无需把一个事务的所有步骤排成一个严格先后执行的序列,可以放松对事务执行步骤全序的要求,接下来定义事务的偏序:
设$A$为任意一个集合,$R \subseteq A \times A$,如果对于任意的元素$a, b, c \in A$,下面三个关系都满足,则称关系$R$是集合$A$上的一个偏序:
- $(a, a) \in R$ 自反性
- $(a, b) \in R \wedge (b,a) \in R \Rightarrow a = b$ 反对称性
- $(a, b) \in R \wedge (b,c) \in R \Rightarrow (a,c) \in R$ 传递性
偏序是全序的一个特例,全序在偏序的定义上又增强了约束,即对于任意两个不同的元素$a, b \in A$,或者$(a,b) \in R$或者$(b,a) \in R$,也就是说对两个不同的数据操作在事务集合中的顺序满足唯一约束。
下面根据偏序定义可以给出在页模型下的事务定义:
一个事务$t$是具体有$r(x)$或$w(x)$形式的多个操作步骤的偏序集合,其中$x \in D$,对同一个页数据的读写操作和写写操作是有序的,正式的,事务可以表示为一个二元组:
$$
t=(op, <)
$$
其中,$op$是具有$r(x)$或者$w(x)$的有限集合,$x \in D$且$x< \subseteq op \times op$是在$op$集合上的偏序关系,如果${p,q} \subseteq op$且$p, q$都对同一个页数据项进行访问,且$p,q$是少有一个是写操作,则有$p < q \wedge q < p$。
根据页事务模型的数学定义可推理出,偏序关系下,不允许同一数据项的读写操作或者写写操作乱序。
对象模型
对象模型可以认为是页模型的替代或者推广,实际上,页模型是隐含在对象模型中。对象模型提供了一个表达在任意类型对象上进行的操作框架,而处于提高性能的需要,可能还需要利用被调用操作的语义。实际上,在一个对象及其操作的实现过程中,是需要调用底层对象的操作。
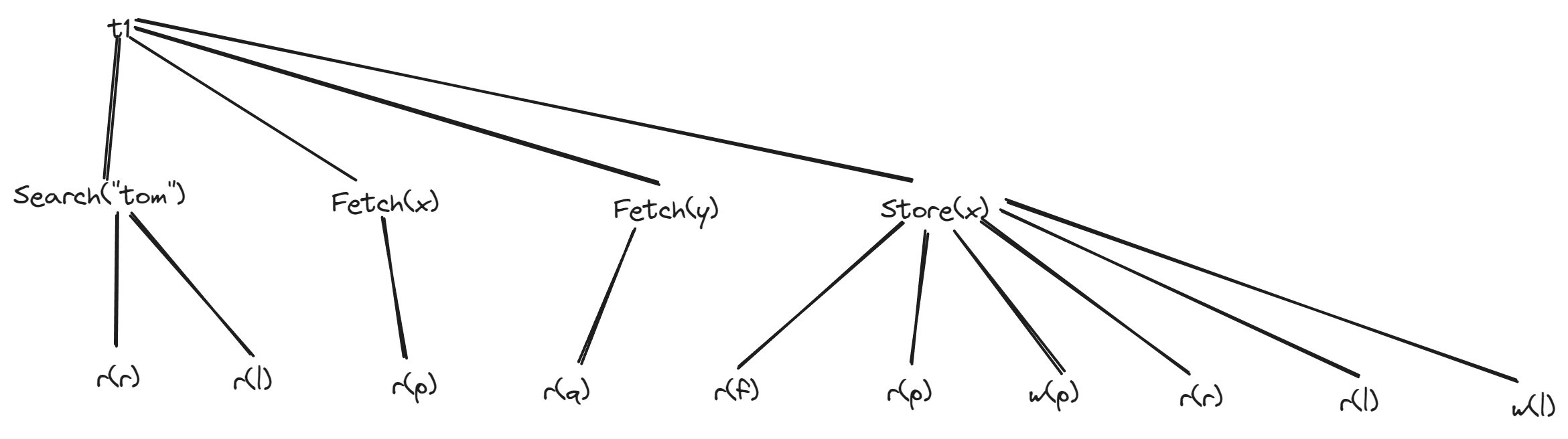
例如在数据库访问层中,比如索引查找,需要调用存储层面向页的操作,类似的调用层次还在业务对象集合中。上图中描述了一个事务,标记为$t_1$,执行了一个SQL的Select语句,从数据库中获取所有名叫“tom”的人员信息,在获取结果后,执行一个SQL语句插入一个新信息。
SQL语句在SQL引擎侧已经被转化为查询处理层的操作。在这个例子中,假设包含两个记录$x$和$y$,查询操作调用存储层的读写页操作。这里假设要读B+树的根节点,并且简单起见,只有两层。叶子节点标记为$l$,其中包含所有符合“tom”的列表,通过主键获取满足条件的记录$x$和$y$,访问每个记录各需要一次页读取,页分别记为$p$和$q$,最后还需要调用一个SQL的Insert语句插入新的信息:首先读取存储层的元数据页,找到有足够空闲的页$p$,读取页$p$,把要插入的记录写入,然后写回该页,最后还要在索引上把新记录的主键加入到B+树上名字叫“tom”的列表中。
上述例子中,实际上是把事务看作一棵树,而被调用的操作作为树节点,为了保证事务树是独立的并且允许严格推理,要求事务树的叶节点必须是页模型的基本读写操作。如果一个给定事务树的叶节点全部或者部分与页读写不对应,唯一能做的就是扩展这棵树把叶子节点全部变成页读写操作。
而这种扩展是动态的,跟踪在执行过程中一个高级事务中的所有低级数据操作,而不是从操作的静态结构生成的一个调用层次图。而跟踪一个事务内部操作的顺序,一种简单的方法就是给所有的叶节点确定一个顺序,和上述图中从左到右的事务顺序一致。所以像页模型一样,也同样要求事务树的所有叶节点保持偏序关系。
现在可以正式给出对象模型事务的定义:
一个事务$t$是一棵有限树,节点进行如下标记:
- 事务标识符来标记根节点;
- 被调用操作的名称和参数标记内部非叶非根节点;
- 页模型的读写操作标记叶子节点;
在叶子节点上定义了偏序关系“$<$”,使得所有的叶子节点操作$p,q$,其中$p$形如$w(x)$, q形如$r(x) \wedge w(x)$,或相反,都满足$p < q \vee q < p$。
对象模型中事务对应的树不一定是平衡的,也就是说从根节点到所有叶子节点的路径不一定是等长的,而为了清晰起见,讨论问题时把属于同样对象操作类型或者接口的操作放在事务树的同层,所以当后续利用对象模型考虑并发执行时,经常放在完全平衡的事务树中。
这种事务树所有叶节点到根节点的路径是等长的,成为分层事务或者多级事务。
在上述的讨论中,有一个问题被忽略了,偏序只在树的叶子节点被提及和定义。内部节点的顺序实际上在叶子节点被约束后已经被隐式定义了。例如,对两个内部节点操作$a$和$b$,如果在叶子节点偏序“<”下,$a$节点下的所有后代叶子节点先于$b$节点下的所有后代叶子节点处理,则称$a$先于$b$,这需要后代叶子节点集合之间有序,否则称$a$和$b$是并发操作。如果想找到中间节点对存储引擎的数据影响,可以检查其子女节点以及更远后代之间的交叉情况,直到叶子节点,其中的偏序关系保证了数据解释的明确性。
最后简要的阐述后续系列如何使用引入的对象模型作为高级并发控制算法的基础来结束本节。当考虑多个事务以并发或者并行的方式执行时,要把所有的事务树组合,形成一个操作的森林,然后检查叶子节点之间的偏序关系,以及隐含推导出来的高层操作顺序。与单层事务不同的是,需要在所有事务树的所有叶子节点集合上来定义偏序关系。而由于内部节点之间的顺序可以由叶子节点的偏序关系推导,可以研究高层节点之间的并发或者并行。而增强事务性能的关键,是高层内部节点操作的语义特性纳入事务调度的考虑范围。
数据库事务模型分析(1)—— 计算模型

